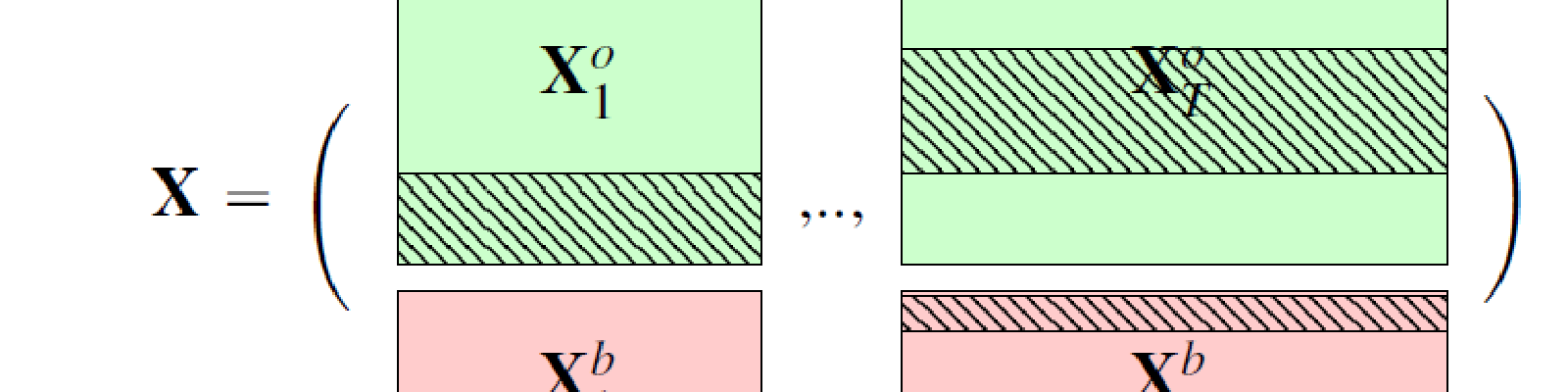
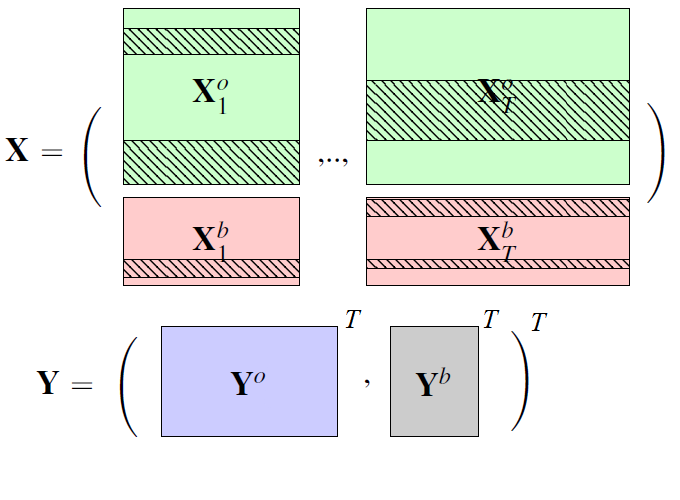
In the high dimensional settings, a large number of variables, one objective is to select the relevant variables and thus to reduce the dimension. That subspace selection is often managed with supervised tools. However, some data can be missing, compromising the validity of the sub-space selection. We propose a Partial Least Square (PLS), flavored method, called Multi-Block Data-Driven sparse PLS (mdd-sPLS), allowing jointly variable selection and subspace estimation while training and testing missing data imputation through a new algorithm called Koh-Lanta. This method was challenged through simulations against existing methods such as mean impute, nipals, softImpute and imputeMFA. A common criterion was used to compare imputation convergence properties: the individual relative position stabilization in the optimization processes. The application of the supervised multi-block mdd-sPLS method to a rVSV-ZEBOV Ebola vaccine trial dataset revealed interesting and biologically consistent results.
I work on this project with Rodolphe Thiébaut and Jérôme Saracco which are my PhD-thesis advisors. That project is in fact my PhD project. It permits me to deal with a large variety of statistical tools and mathematical concepts but also with algorithms problems.
CRAN-R-package, GitHub-R-package,
PyPi-Python-package, GitHub-Python-package.
The preprint is available on arXiv.